
Wednesday, January 2, 2019
I ran into a graph problem a while back, and finally decided to write about it.
One day I'll write a bdlat-compatible C++ class
generator. It will allow you to write things like basic.bdlat:
(package basic
(import core)
(type Value
"a generic value in a restricted type system"
(choice
("integer" core/integer)
("decimal" core/decimal)
("string" core/string)
("optional" (optional Value))
("array" (array Value))))
and then do something like
$ bat-codegen --language c++ --toplevel Lakos --component types basic.bdlat
to produce the files basic_types.h and basic_types.cpp containing the C++
class Lakos::basic::Value.
Here's a first shot at what the definition of Lakos::basic::Value might look
like:
class Value {
bdlb::Variant<int64_t,
bdldfp::Decimal64,
bsl::string,
bdlb::NullableValue<Value>,
bsl::vector<Value> >
d_data;
public:
// ...
};
A real implementation would need to account for choice elements having the same
type, and so the types in the Variant would each have to be tagged with a
distinct integer, but let's ignore that for now.
We've already run into worse trouble, because this code won't even compile.
Value's size depends on its own size. To work around this, a level of
indirection is needed. Suppose the class template Allocated<T> were a
wrapper around a heap-allocated T referred to by a T*, but with value
semantics rather than pointer semantics (i.e. copying the Allocated<T>
copies the referred to T instance). Then Value can be defined as:
class Value {
bdlb::Variant<int64_t,
bdldfp::Decimal64,
bsl::string,
Allocated<bdlb::NullableValue<Value> >,
Allocated<bsl::vector<Value> > >
d_data;
public:
// ...
};
That would work, because Allocated<T>'s size is independent of T.
When a type depends upon itself, it doesn't necessarily do so by having itself
as a member (as was nearly the case with Value above). It could be that the
type contains a type that contains the original type. Or it could be that the
type contains a type that contains a type that contains the original type, etc.
Generally, a type A contains a type B if any of the following is true:
A is a sequence or a choice having an element of type BA is a sequence or a choice having an element of type (optional B)A is a sequence or a choice having an element of type (array B)We can think of a set of types as a directed graph where an edge points from
A to B if A contains B. Let's call such a directed graph a dependency
graph.
Then A depends upon B if A contains B or if A contains a C
where C depends upon B. That is, A depends upon B if there exists a
directed path from A to B in the dependency graph.
The graph for the types in (package basic ...), above, looks like this:

It has one vertex and one edge, from Value to itself: because (before our
modification) Value contains Value. Our modification, though, creates
a level of indirection: replacing Value with Allocated<Value> within the
class definition removes the one edge in the graph, since Value no longer
contains Value:

A cycle involving only one vertex is not very interesting. But suppose the dependency graph looked like this instead:
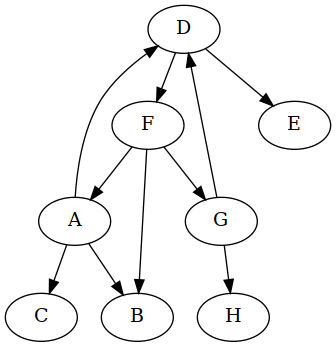
How many cycles does that directed graph contain? I see two:
As before, we wish to make this directed graph acyclic by removing edges, where
we remove an edge by replacing the appearance of a type T within a class
definition with Allocated<T>.
Which edges should be removed?
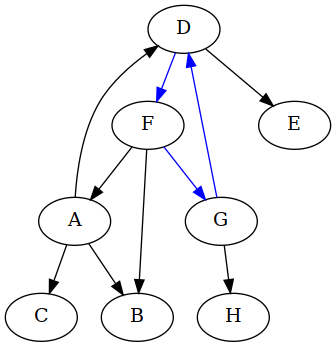
Perhaps only because of the way the graph is drawn, I'm tempted to think of the
vertex D as the "main" type in the schema, and that makes me want to remove
the two edges inbound into it:
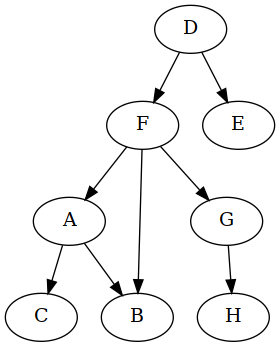
The graph now has no cycles. In fact, it would be a tree were it not for B
having two parents (A and F). Also, note that since this is a directed
graph, the edge sequence FA, AB, BF is not a path, and thus not a
cycle, because the edge between B and F goes from F to B, not the
other way around.
What we did from the C++ point of view is go into the definitions of the A
and G classes and replace all appearances of D with Allocated<D>.
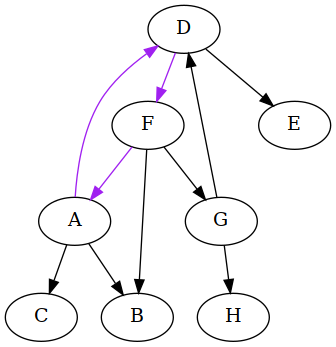
You might have noticed that there is another way we could have broken the cycles. Here's the original cyclic graph again:

Both cycles share an edge, DF, and removing just that one breaks both
cycles:
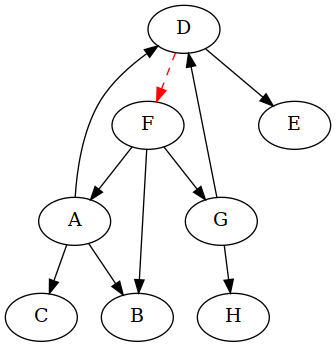

Now graphviz wants to put F on top, interesting.
What's the difference between the two de-cyclings demonstrated above? My first
thought was that less is more, and so removing the cycles by adding only one
Allocated<T> is better than adding two. That's not a fully reasoned argument,
though.
It's true that there is a cost associated with the level of indirection
introduced by Allocated<T>. Whenever you want to read or write to
something in that member, you have to chase a pointer, rather than just work
at an offset from the parent object. Also, when the Allocated<T> is
created, it must allocate space for the T. That cost might or might not
be significant depending on how memory is allocated.
How much is the total cost, though? Suppose that we replaced every member
of every class with Allocated<T>, as is done in dynamic and "object
oriented" languages. Would a running program notice the difference? Would
all the concern about "cache friendliness" matter?
Here's another thought. If the object of type T that you are replacing with an
Allocated<T> is much larger than Allocated<T> on the stack, and if access to
that T would have been infrequent anyway, it might actually be advantageous
to "tuck away" the rarely accessed member to allow adjacent objects to remain
in cache more often.
Nothing but a good suite of benchmarks could answer these questions.
Still, we have to at least get the code to compile. Making everything an
Allocated<T> seems at least unnecessary, if not detrimental. How, then, do
we decide which edges to remove from our cyclic graphs?
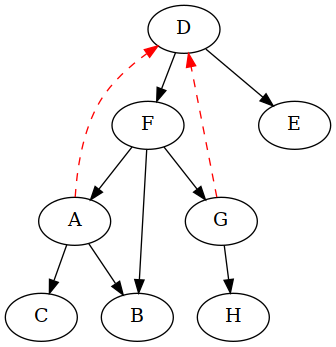
Simple but suboptimal would be to say: "Any type that appears in a cycle must
be referred to only by Allocated<T>." This makes certain that all cycles are
removed, but potentially introduces many more Allocated<T> than necessary.
In the previous example, it would mean removing five edges instead of one:
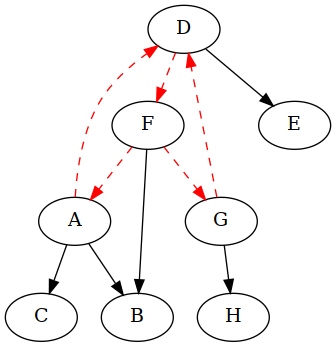
Also, if there were edges coming in from other vertices into any of the vertices
A, D, F, or G, those edges too would be removed, even though they aren't
part of either cycle.
It seems a waste, but on the other hand, maybe it's simple to implement: just walk through the graph with a clipboard, noting all of the nodes appearing in cycles, and you're done. Surprisingly, enumerating all of the cycles in a directed graph efficiently is nontrivial.
The problem is that there can be an awful lot of cycles in a directed graph. A complete directed graph having n vertices and ~n2 edges can have up to this many (simple) cycles:
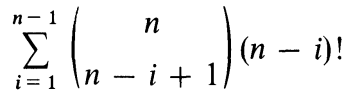
That's way more than 2n, so at worst we're totally screwed.
Fortunately, no schema describing C++ classes is going to have a complete dependency graph. Even if it were complete, then n would be small.
So, the shotgun method of "Allocated<T> for every T appearing in a cycle" is
still on the table, but can we do better?
What about the smallest set of edges we'd need to remove to make the
dependency graph acyclic? How do we calculate that set? In the example, above,
the answer is just the one edge DF — we can't remove zero edges, and
removing the one edge DF does the trick, and so that must be the smallest
set (assuming there is no other single edge that could be removed instead, and
there isn't).
The problem of finding the size (cardinality) of a minimal set of edges to remove from a cyclic directed graph to render it acyclic is called the minimum feedback arc set problem, and it's NP-complete, which sucks.
Apparently the solution can be approximated to an arbitrary level of accuracy, but unless I find a tested implementation of one of the approximate or complete solutions in an off-the-shelf graph library, I'm not about to implement it myself for a code generator.
I've come up with an algorithm that spits out a set of edges to remove from a
directed graph to render it acyclic, and as far as I can reason its worse case
time complexity is a polynomial in n, the number of vertices, and e, the
number of edges.
Now, maybe I'm wrong about that complexity, but regardless, either the algorithm is more complex than I think, or it's doesn't always find the minimum feedback arc set (or both). Because P ≠ NP. Probably.
Still seems pretty good to me, though. Here's how it works.
The idea is to do a depth-first search for "cyclic edges," trying multiple times, once for each vertex. The result is then the smallest of the sets of "cyclic edges" found. If there multiple disconnected subgraphs, then the result is the smallest union of the results from all subgraphs.
Choose a starting vertex, say, A. Walk the directed graph depth-first,
keeping track of ancestor nodes using a hash set s (i.e. add nodes "on the
way down" and remove them "on the way back up" — or mark the vertices in
place, if possible).
If you re-encounter an ancestor in your set s while traversing the graph,
note which edge brought you to the ancestor, take a step back (across that
edge) and then proceed as if that edge did not exist. That edge is what I called
a "cyclic edge," above.
This procedure will give you a set of edges removed from the graph in order
to make it acyclic from A's point of view.
The hunch of this algorithm is that if you repeat the procedure starting at each other vertex as well, then maybe you'll stumble upon the minimum feedback arc set.
Here is an animated example using the same graph we've been using.
Start at vertex A and do a depth-first traversal until you run into trouble:
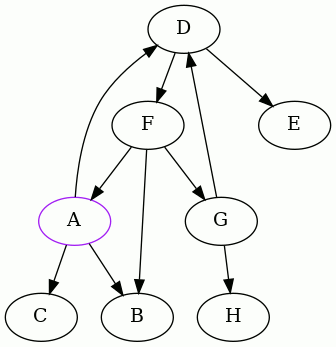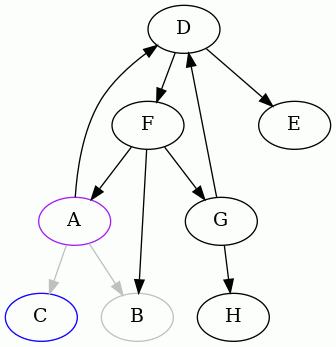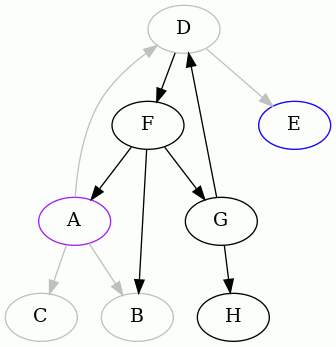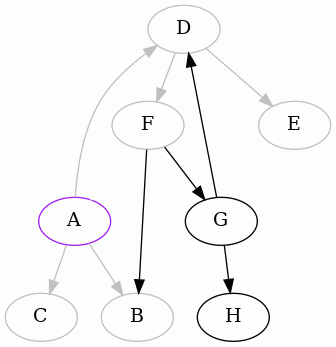
In these animations, the purple (pink) node is the one from which we started,
blue indicates the edge or vertex we're currently examining, and gray indicates
an edge or vertex that we've already visited. Red marks edges that lead to a
vertex in the current set s of ancestors.
We detected that the edge FA creates a cycle, so we remember it, remove it,
and continue:

We detected that the edge GD creates a cycle, and so we did as before. Now
there's little left to do, from A's point of view:

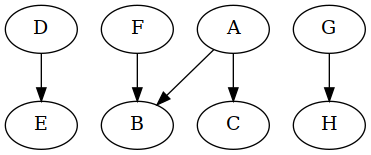
Thus the following two edges were removed to make the graph acyclic, starting
from A:

Next we do the whole thing over, but this time starting from B. Starting from
B or C is not very interesting, since they're both leaves. The algorithm,
having run out of tree at B and noticing that there were still unvisited
edges, would proceed starting from another vertex, say, A. But we already did
A. So this adds no new information.
The next interesting vertex to start from, alphabetically, is D. Here is the
complete animation starting from D, and then the resulting edges removed:
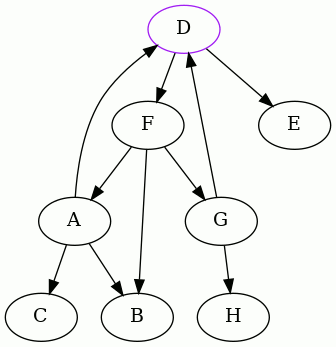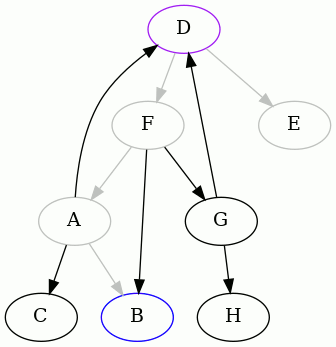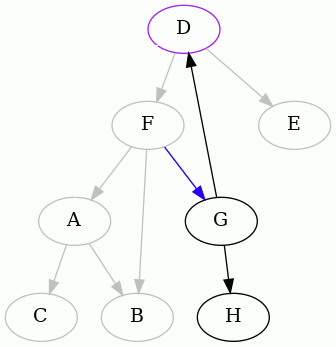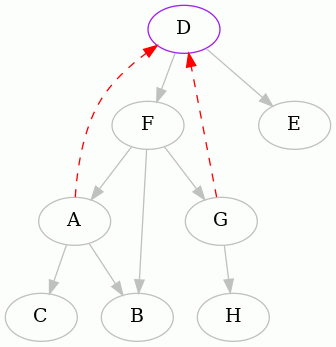
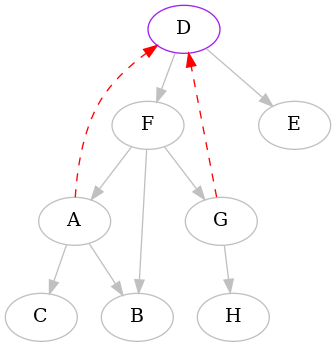
As you can see, one of the edges is different than before.
The punchline is the result starting from F. Here it is:
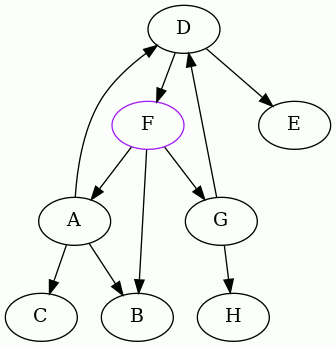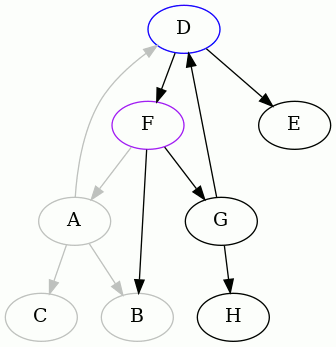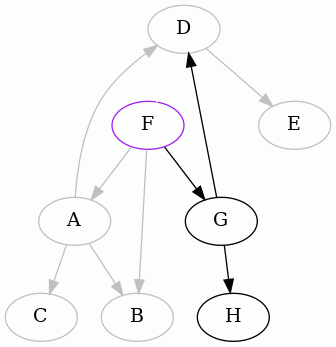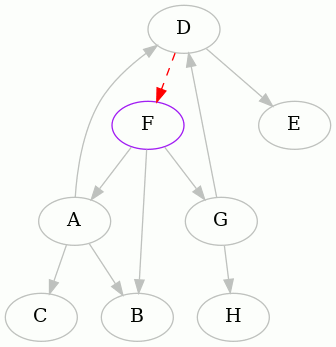

So we discover that the minimum feedback arc set of this directed graph is
{DF}.
As I said before, this algorithm can't be right. What might help is a test suite that randomly generates directed graphs, and then compares the result of this algorithm with the result of brute-force checking the power set of the graph's edges. I could hope to find a counter-example that way, though none very large, since the brute force solution is exponential in the number of edges.